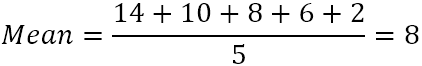Как рассчитать дисперсию в Excel — формула дисперсии выборки и генеральной совокупности
В этом уроке мы рассмотрим, как проводить дисперсионный анализ в Excel и какие формулы использовать для нахождения дисперсии выборки и генеральной совокупности.
Дисперсия — один из самых полезных инструментов в теории вероятностей и статистике. В науке он описывает, насколько далеко каждое число в наборе данных от среднего. На практике это часто показывает, насколько сильно что-то меняется. Например, температура вблизи экватора имеет меньшую дисперсию, чем в других климатических зонах. В этой статье мы проанализируем различные методы расчета дисперсии в Excel.
Что такое дисперсия?
Дисперсия — это мера изменчивости набора данных, которая указывает, насколько далеко разбросаны разные значения. Математически он определяется как среднее квадратов отличий от среднего.
Чтобы лучше понять, что вы на самом деле рассчитываете с помощью дисперсии, рассмотрите этот простой пример.
Предположим, в вашем местном зоопарке есть 5 тигров в возрасте 14, 10, 8, 6 и 2 лет.
Чтобы найти дисперсию, выполните следующие простые шаги:
- Вычислите среднее (простое среднее) пяти чисел:

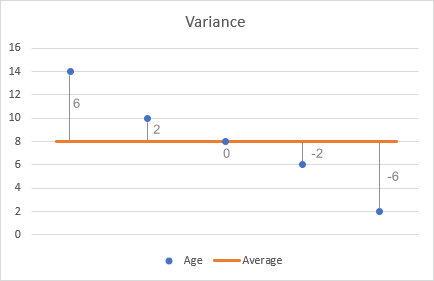
- Из каждого числа вычтите среднее значение, чтобы найти различия. Для наглядности нанесем различия на график:

- Сократите каждую разницу.
- Вычислите среднее квадратов разностей.
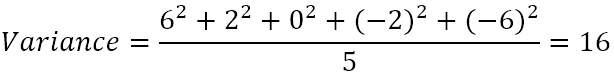
Итак, дисперсия равна 16. Но что на самом деле означает это число?
По правде говоря, дисперсия просто дает вам очень общее представление о дисперсии набора данных. Значение 0 означает отсутствие изменчивости, т. е. все числа в наборе данных одинаковы. Чем больше число, тем больше разбросаны данные.
Этот пример для дисперсия населения (т.е. 5 тигров — это вся интересующая вас группа). Если ваши данные являются выборкой из большей совокупности, вам необходимо рассчитать выборочная дисперсия по несколько иной формуле.
Как посчитать дисперсию в Excel
В Excel есть 6 встроенных функций для расчета дисперсии: VAR, VAR.S, VARP, VAR.P, VARA и VARPA.
Ваш выбор формулы дисперсии определяется следующими факторами:
- Версия Excel, которую вы используете.
- Независимо от того, рассчитываете ли вы выборку или дисперсию населения.
- Хотите ли вы оценивать или игнорировать текст и логические значения.
Функции дисперсии Excel
В таблице ниже представлен обзор функций вариации, доступных в Excel, которые помогут вам выбрать формулу, наиболее подходящую для ваших нужд.
Название Версия Excel Тип данных Текст и логика
БЫЛ
2000 – 2019 Образец игнорируется
ЧЬЯ
2010 – 2019 Образец игнорируется
БЫТЬ
2000 – 2019 Образец Оценка
ПОСЛЕДНИЙ
2000–2019 гг. Население не учитывается
ДА
2010–2019 гг. Население не учитывается
БРОСАТЬ
2000 – 2019 Оценка населения
ВАР.С против. ВАРА и ВАР.П vs. ДЕФОРМАЦИЯ
VARA и VARPA отличаются от других функций дисперсии только тем, как они обрабатывают логические и текстовые значения в ссылках. В следующей таблице приведены сводные данные о том, как оцениваются текстовые представления чисел и логических значений.
Тип аргумента VAR, VAR.S, VARP, VAR.P VARA и VARPA Логические значения в массивах и ссылках Игнорируется Оценивается
(TRUE=1, FALSE=0) Текстовые представления чисел в массивах и ссылках Игнорируется Оценивается как ноль Логические значения и текстовые представления чисел, вводимые непосредственно в аргументы Оцениваются
(TRUE=1, FALSE=0) Пустые ячейки Игнорируются
Как рассчитать выборочную дисперсию в Excel
Выборка представляет собой набор данных, извлеченных из всего населения. А дисперсия, рассчитанная по выборке, называется выборочной дисперсией.
Например, если вы хотите узнать, как меняется рост людей, для вас будет технически невозможно измерить каждого человека на земле. Решение состоит в том, чтобы взять выборку населения, скажем, 1000 человек, и оценить рост всего населения на основе этой выборки.
Выборочная дисперсия рассчитывается по следующей формуле: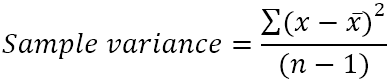
Где:
- x̄ – среднее (простое среднее) значений выборки.
- n — размер выборки, т. е. количество значений в выборке.
В Excel есть 3 функции для нахождения выборочной дисперсии: VAR, VAR.S и VARA.
Функция ВАР в Excel
Это самая старая функция Excel для оценки дисперсии на основе выборки. Функция VAR доступна во всех версиях Excel с 2000 по 2019.
ВАР(число1, [number2]…)
Примечание. В Excel 2010 функция VAR была заменена функцией VAR.S, которая обеспечивает повышенную точность. Хотя VAR по-прежнему доступен для обратной совместимости, рекомендуется использовать VAR.S в текущих версиях Excel.
Функция VAR.S в Excel
Это современный аналог функции Excel VAR. Используйте функцию VAR.S, чтобы найти выборочную дисперсию в Excel 2010 и более поздних версиях.
ВАР.С(число1, [number2]…)
Функция ВАРА в Excel
Функция Excel VARA возвращает примерную дисперсию на основе набора чисел, текста и логических значений, как показано на рис. этот стол.
БЫТЬ(значение1, [value2]…)
Пример формулы отклонения в Excel
При работе с числовым набором данных вы можете использовать любую из вышеперечисленных функций для расчета выборочной дисперсии в Excel.
В качестве примера найдем дисперсию выборки, состоящей из 6 элементов (B2:B7). Для этого можно использовать одну из следующих формул:
= ПЕРЕМ(B2:B7)
=ПЕР.С(B2:B7)
=ВАРА(B2:B7)
Как показано на скриншоте, все формулы возвращают один и тот же результат (округленный до 2 знаков после запятой):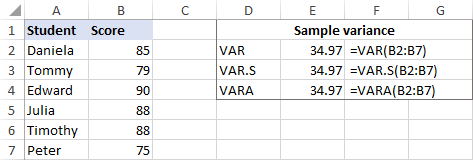
Чтобы проверить результат, произведем расчет var вручную:
- Найдите среднее значение с помощью функции СРЗНАЧ:
=СРЕДНЕЕ(B2:B7)Среднее значение идет в любую пустую ячейку, скажем, B8.
- Вычтите среднее значение из каждого числа в выборке:
=B2-$B$8Различия идут в столбец C, начиная с C2.
- Возведите в квадрат каждую разницу и поместите результаты в столбец D, начиная с D2:
=С2^2 - Сложите квадраты разностей и разделите результат на количество элементов в выборке минус 1:
=СУММ(D2:D7)/(6-1)
Как видите, результат нашего ручного вычисления var точно такой же, как число, возвращаемое встроенными функциями Excel: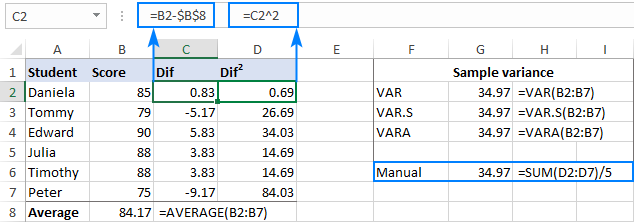
Если ваш набор данных содержит логические и/или текстовые значения, функция VARA вернет другой результат. Причина в том, что VAR и VAR.S игнорируют любые значения, отличные от чисел, в ссылках, в то время как VARA оценивает текстовые значения как нули, TRUE как 1 и FALSE как 0. Поэтому, пожалуйста, тщательно выбирайте функцию дисперсии для своих расчетов в зависимости от того, хотите обработать или игнорировать текст и логические операции.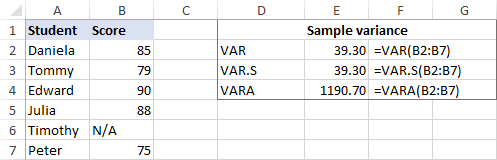
Как рассчитать дисперсию населения в Excel
Совокупность – это все члены данной группы, т. е. все наблюдения в области исследования. Дисперсия населения описывает, как распределены точки данных во всей совокупности.
Дисперсию населения можно найти по следующей формуле: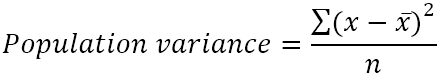
Где:
- x̄ – среднее значение населения.
- n — размер совокупности, т. е. общее количество значений в совокупности.
В Excel есть 3 функции для расчета дисперсии генеральной совокупности: VARP, VAR.P и VARPA.
Функция VARP в Excel
Функция Excel VARP возвращает дисперсию генеральной совокупности на основе всего набора чисел. Он доступен во всех версиях Excel с 2000 по 2019.
ВАРП(число1, [number2]…)
Примечание. В Excel 2010 VARP был заменен на VAR.P, но по-прежнему сохранен для обратной совместимости. В текущих версиях Excel рекомендуется использовать ДИСП.П, поскольку нет гарантии, что функция ДИСП будет доступна в будущих версиях Excel.
Функция VAR.P в Excel
Это улучшенная версия функции VARP, доступная в Excel 2010 и более поздних версиях.
ВАР.П(число1, [number2]…)
Функция ДСПСП в Excel
Функция VARPA вычисляет дисперсию генеральной совокупности на основе всего набора чисел, текста и логических значений. Он доступен во всех версиях Excel с 2000 по 2019.
БЫТЬ(значение1, [value2]…)
Формула дисперсии населения в Excel
в пример расчета переменной, мы обнаружили расхождение в 5 экзаменационных баллов, предполагая, что эти баллы были выбраны из большей группы студентов. Если вы соберете данные обо всех учащихся в группе, эти данные будут представлять все население, и вы рассчитаете дисперсию населения, используя вышеуказанные функции.
Допустим, у нас есть экзаменационные баллы группы из 10 студентов (B2:B11). Баллы составляют всю совокупность, поэтому мы будем делать дисперсию с этими формулами:
=СКОРБКА(B2:B11)
=ПЕР.П(B2:B11)
=ТОЭ(B2:B11)
И все формулы вернут одинаковый результат: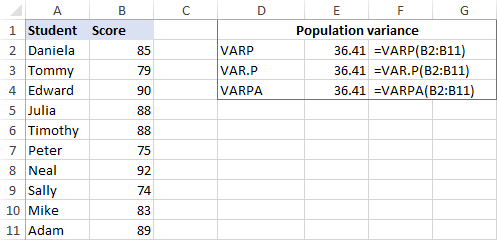
Чтобы убедиться, что Excel правильно рассчитал дисперсию, вы можете проверить ее с помощью формулы ручного расчета var, показанной на снимке экрана ниже: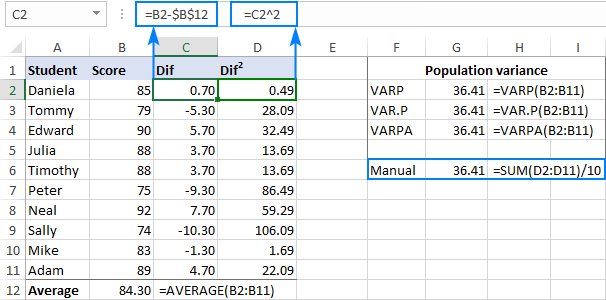
Если кто-то из студентов не сдавал экзамен и вместо количества баллов указано N/A, функция VARPA вернет другой результат. Причина в том, что VARPA оценивает текстовые значения как нули, в то время как VARP и VAR.P игнорируют текстовые и логические значения в ссылках. Посмотри пожалуйста VAR.P vs. БЫЛ НА для получения полной информации.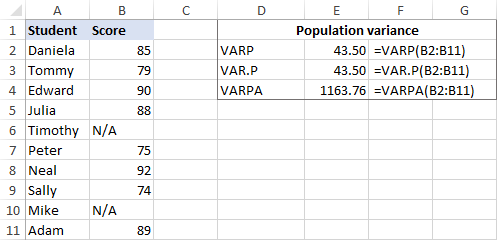
Формула дисперсии в Excel — примечания по использованию
Чтобы правильно провести дисперсионный анализ в Excel, следуйте простым правилам:
- Предоставляйте аргументы в виде значений, массивов или ссылок на ячейки.
- В Excel 2007 и более поздних версиях можно указать до 255 аргументов, соответствующих выборке или генеральной совокупности; в Excel 2003 и старше — до 30 аргументов.
- Чтобы оценить только числа в ссылках, игнорируя пустые ячейки, текст и логические значения, используйте функцию VAR или VAR.S для расчета выборочной дисперсии и VARP или VAR.P для нахождения дисперсии генеральной совокупности.
- Для оценки логических и текстовых значений в ссылках используйте функцию VARA или VARPA.
- Укажите не менее двух числовых значений для формула выборочной дисперсии и по крайней мере одно числовое значение для формула дисперсии населения в Excel, иначе #DIV/0! возникает ошибка.
- Аргументы, содержащие текст, который нельзя интерпретировать как числа, приводят к ошибке #ЗНАЧ! ошибки.
Дисперсия по сравнению со стандартным отклонением в Excel
Дисперсия, несомненно, полезная концепция в науке, но она дает очень мало практической информации. Например, мы нашли возраст популяции тигров в местном зоопарке и рассчитал дисперсиючто равно 16. Вопрос в том, как на самом деле мы можем использовать это число?
Вы можете использовать дисперсию для определения стандартного отклонения, которое является гораздо лучшей мерой количества вариаций в наборе данных.
Стандартное отклонение рассчитывается как квадратный корень из дисперсии. Итак, мы берем квадратный корень из 16 и получаем стандартное отклонение 4.
В сочетании со средним значением стандартное отклонение может сказать вам, сколько лет большинству тигров. Например, если среднее значение равно 8, а стандартное отклонение равно 4, возраст большинства тигров в зоопарке составляет от 4 (8 – 4) до 12 лет (8 + 4).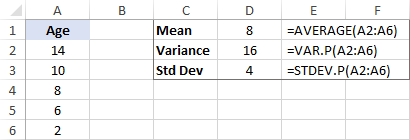
Microsoft Excel имеет специальные функции для расчета стандартного отклонения выборки и генеральной совокупности. Подробное объяснение всех функций можно найти в этом руководстве: Как рассчитать стандартное отклонение в Excel.
Вот как сделать дисперсию в Excel. Чтобы поближе познакомиться с формулами, обсуждаемыми в этом руководстве, вы можете загрузить наш образец рабочей книги в конце этого поста. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Практическая рабочая тетрадь
Вычислить дисперсию в Excel – примеры (файл .xlsx)